

A full treatment of the energy states of each molecule is unfeasible for
molecules larger than diatomics, as there are simply too many states. To
simplify things we apply the RRKM approximation, which leaves the state of a
molecule as a function of two quantities: the total energy 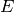 and total
angular momentum quantum number
and total
angular momentum quantum number 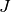 . Frequently we will find that even
this is too difficult, and will only keep the total energy
. Frequently we will find that even
this is too difficult, and will only keep the total energy 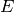 as an
independent variable.
as an
independent variable.
Throughout this document we will utilize the following terminology:
The isomers are the configurations for which we must model the energy states.
We designate 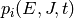 as the population of isomer
as the population of isomer 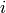 having
total energy
having
total energy 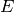 and total angular momentum quantum number
and total angular momentum quantum number 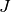 at
time
at
time 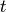 . At long times, statistical mechanics requires that the
population of each isomer approach a Boltzmann distribution
. At long times, statistical mechanics requires that the
population of each isomer approach a Boltzmann distribution 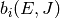 :
:
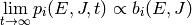
We can simplify by eliminating the angular momentum quantum number to get
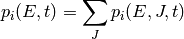
Let us also denote the (time-dependent) total population of isomer 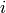 by
by 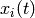 :
:
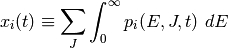
The two molecules of a reactant or product channel are free to move apart from
one another and interact independently with other molecules in the system.
Accordingly, we treat these channels as fully thermalized, leaving as the only
variable the total concentrations 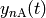 and
and
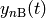 of the molecules
of the molecules 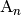 and
and 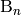 of reactant channel
of reactant channel 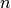 . (Since the product channels act as infinite
sinks, their populations do not need to be considered explicitly.)
. (Since the product channels act as infinite
sinks, their populations do not need to be considered explicitly.)
Finally, we will use 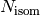 ,
, 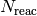 , and
, and
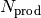 as the numbers of isomers, reactant channels, and
product channels, respectively, in the system.
as the numbers of isomers, reactant channels, and
product channels, respectively, in the system.
Bimolecular collisions with an inert species 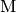 are the primary
means by which an isomer molecule changes its energy. A reasonable estimate –
although generally a bit of an underestimate – of the total rate of collisions
are the primary
means by which an isomer molecule changes its energy. A reasonable estimate –
although generally a bit of an underestimate – of the total rate of collisions
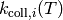 for each isomer
for each isomer 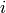 comes from
Lennard-Jones collision theory:
comes from
Lennard-Jones collision theory:
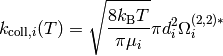
Above, 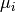 is the reduced mass,
is the reduced mass, 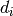 is the collision diameter,
and
is the collision diameter,
and 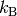 is the Boltzmann constant. The collision diameter is
generally taken as
is the Boltzmann constant. The collision diameter is
generally taken as 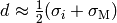 ,
the arithmetic average of the Lennard-Jones
,
the arithmetic average of the Lennard-Jones 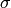 parameter for the
isomer and the bath gas. The parameter
parameter for the
isomer and the bath gas. The parameter 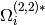 represents
a configurational integral, which is well-approximated by the expression
represents
a configurational integral, which is well-approximated by the expression
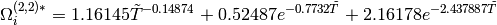
where 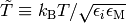 is a reduced temperature and
is a reduced temperature and 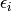 is the Lennard-Jones
is the Lennard-Jones
 parameter. Note that we have used a geometric average for the
parameter. Note that we have used a geometric average for the
 parameters of the isomer and the bath gas in this expression.
Assuming the total gas concentration to be constant and that the gas is ideal,
we obtain an expression for the collision frequency
parameters of the isomer and the bath gas in this expression.
Assuming the total gas concentration to be constant and that the gas is ideal,
we obtain an expression for the collision frequency 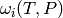 ,
which makes explicit the pressure dependence:
,
which makes explicit the pressure dependence:
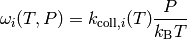
Now that we have an estimate for the total rate of collisions, we need to
develop a model of the effect that these collisions have on the state of the
isomer distribution. To this end, we define
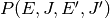 as the probability of a collision
resulting in a transfer of a molecule from state
as the probability of a collision
resulting in a transfer of a molecule from state 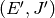 to state
to state 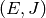 . There are two mathematical constraints on
. There are two mathematical constraints on
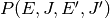 . The first of these is normalization:
. The first of these is normalization:
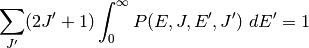
The second of these is detailed balance, required in order to obtain the Boltzmann distribution at long times:
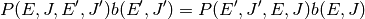
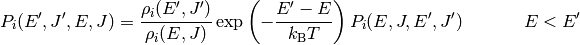
Rather than define models directly for 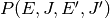 ,
we usually eliminate the angular momentum contribution and instead define
,
we usually eliminate the angular momentum contribution and instead define
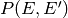 . This can be related to
. This can be related to
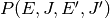 via
via
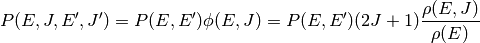
where 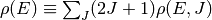 .
.
There are a variety of models used for 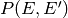 .
By far the most common is the single exponential down model
.
By far the most common is the single exponential down model
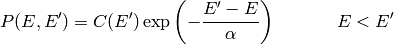
where 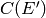 is determined from the normalization constraint. Note
that this function has been defined for the deactivating direction
(
is determined from the normalization constraint. Note
that this function has been defined for the deactivating direction
(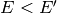 ) only, as the activating direction (
) only, as the activating direction (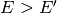 )
is then set from detailed balance. The parameter
)
is then set from detailed balance. The parameter 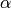 corresponds to
the average energy transferred in a deactivating collision
corresponds to
the average energy transferred in a deactivating collision
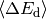 , which itself is a weak function of
temperature.
, which itself is a weak function of
temperature.
Other models for 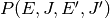 include the Gaussian down
include the Gaussian down
![P(E, E^\prime) = C(E^\prime) \exp \left[ - \frac{(E^\prime - E)^2}{\alpha^2} \right] \hspace{40pt} E < E^\prime](../_images/math/52e939085ae923c0677d57140221b23e655c3a37.png)
and the double exponential down
![P(E, E^\prime) = C(E^\prime) \left[ (1 - f) \exp \left( -\frac{E^\prime - E}{\alpha_1} \right) + f \exp \left( -\frac{E^\prime - E}{\alpha_2} \right) \right] \hspace{40pt} E < E^\prime](../_images/math/0d1518c249dabed47fad8b21eef9402540977038.png)
The parameters for these simple models generally contain so much uncertainty that more complex functional forms are generally not used.
Chemical reaction events cause a change in molecular configuration at constant
energy. The rate coefficient for this process must be determined as a function
of energy rather than the usual temperature. Such a quantity is called a
microcanonical rate coefficient and written as 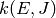 . In the master
equation we will differentiate between microcanonical rate coefficients for
isomerization, dissociation, and association by using different letters:
. In the master
equation we will differentiate between microcanonical rate coefficients for
isomerization, dissociation, and association by using different letters:
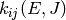 for isomerization,
for isomerization, 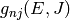 for dissociation,
and
for dissociation,
and 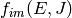 for association. (By convention, we use indices
for association. (By convention, we use indices
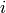 and
and 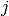 to refer to unimolecular isomers,
to refer to unimolecular isomers, 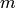 and
and
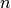 to refer to bimolecular reactant and product channels, and, later,
to refer to bimolecular reactant and product channels, and, later,
 and
and  to refer to energy grains.)
to refer to energy grains.)
As with collision models, the values of the microcanonical rate coefficients are constrained by detailed balance so that the proper equilibrium is obtained. The detailed balance expressions have the form
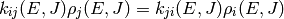
for isomerization and
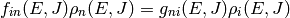
for association/dissociation, where 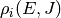 is the density of
states of the appropriate unimolecular or bimolecular configuration.
is the density of
states of the appropriate unimolecular or bimolecular configuration.
An alternative formulation incorporates the macroscopic equilibrium coefficient
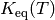 and equilibrium distributions
and equilibrium distributions 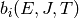 at
each temperature:
at
each temperature:
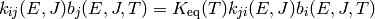
for isomerization and
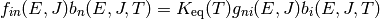
for association/dissociation. Note that these two formulations are equivalent if the molecular degrees of freedom are consistent with the macroscopic thermodynamic parameters. There are multiple reasons to use the latter formulation:
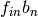 , and not
the individual values of
, and not
the individual values of 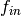 and
and 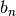 .
.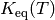 .
.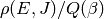 . For example, if
the external rotational constants are unknown then we will include an active
K-rotor in the density of states; this property means that the rotational
constant of this active K-rotor cancels and is therefore arbitrary.
. For example, if
the external rotational constants are unknown then we will include an active
K-rotor in the density of states; this property means that the rotational
constant of this active K-rotor cancels and is therefore arbitrary.There are two common ways of determining values for 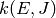 : the
inverse Laplace transform method and RRKM theory. The latter requires detailed
information about the transition state, while the former only requires the
high-pressure limit rate coefficient
: the
inverse Laplace transform method and RRKM theory. The latter requires detailed
information about the transition state, while the former only requires the
high-pressure limit rate coefficient 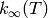 .
.
The microcanonical rate coefficient 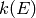 is related to the canonical
high-pressure limit rate coefficient
is related to the canonical
high-pressure limit rate coefficient 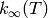 via a Boltzmann
averaging
via a Boltzmann
averaging
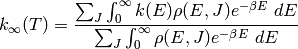
where 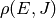 is the rovibrational density of states for the
reactants and
is the rovibrational density of states for the
reactants and 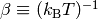 . Neglecting the
angular momentum dependence, the above can be written in terms of Laplace
transforms as
. Neglecting the
angular momentum dependence, the above can be written in terms of Laplace
transforms as
![k_\infty(T) = \frac{\mathcal{L} \left[ k(E) \rho(E) \right]} {\mathcal{L} \left[ \rho(E) \right]} = \frac{\mathcal{L} \left[ k(E) \rho(E) \right]} {Q(\beta)}](../_images/math/5dc2d3e782e16d125cd9b79b722e50faa4754c70.png)
where 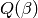 is the rovibrational partition function for the
reactants. The above implies that
is the rovibrational partition function for the
reactants. The above implies that 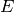 and
and 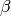 are the transform
variables. We can take an inverse Laplace transform in order to solve for
are the transform
variables. We can take an inverse Laplace transform in order to solve for
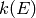 :
:
![k(E) = \frac{\mathcal{L}^{-1} \left[ k_\infty(\beta) Q(\beta) \right] }{\rho(E)}](../_images/math/bc169a8eb75af9f5ca770ea2b052da4350882090.png)
Hidden in the above manipulation is the assumption that 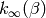 is valid over a temperature range from zero to positive infinity.
is valid over a temperature range from zero to positive infinity.
The most common form of 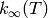 is the modified Arrhenius expression
is the modified Arrhenius expression
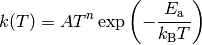
where 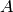 ,
, 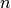 , and
, and 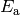 are the Arrhenius
preexpoential, temperature exponent, and activation energy, respectively. For
are the Arrhenius
preexpoential, temperature exponent, and activation energy, respectively. For
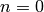 and
and 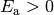 the inverse Laplace transform can be
easily evaluated to give
the inverse Laplace transform can be
easily evaluated to give
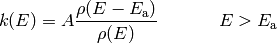
We can also determine an expression when 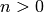 and
and
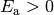 using a convolution integral:
using a convolution integral:
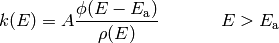
![\phi(E) = \mathcal{L}^{-1} \left[ T^n Q(\beta) \right] = \frac{1}{k_\mathrm{B}^n \Gamma(n)} \int_0^E (E - x)^{n-1} \rho(x) \ dx](../_images/math/646b45318080adab8cee9e95a6365c6ae9b7830a.png)
Finally, for cases where 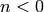 and/or
and/or 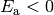 we
obtain a rough estimate by lumping these contributions into the preexponential
at the temperature we are working at. By redoing this at each temperature being
considered we minimize the error introduced, at the expense of not being able
to identify a single
we
obtain a rough estimate by lumping these contributions into the preexponential
at the temperature we are working at. By redoing this at each temperature being
considered we minimize the error introduced, at the expense of not being able
to identify a single 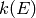 .
.
RRKM theory – named for Rice, Ramsperger, Kassel, and Marcus – is a microcanonical transition state theory. Like canonical transition state theory, detailed information about the transition state and reactants are required, e.g. from a quantum chemistry calculation. If such information is available, then the microcanonical rate coefficient can be evaluated via the equation
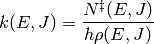
where 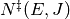 is the sum of states of the transition state,
is the sum of states of the transition state,
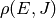 is the density of states of the reactant, and
is the density of states of the reactant, and 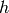 is
the Planck constant. Both the transition state and the reactants have been
referenced to the same zero of energy. The sum of states is related to the
density of states via
is
the Planck constant. Both the transition state and the reactants have been
referenced to the same zero of energy. The sum of states is related to the
density of states via
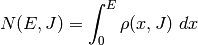
The angular momentum quantum number dependence can be removed via
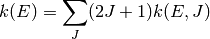
The governing equation for the population distributions 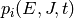 of each isomer
of each isomer 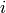 and the reactant concentrations
and the reactant concentrations
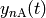 and
and 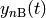 combines the
collision and reaction models to give a linear integro-differential equation:
combines the
collision and reaction models to give a linear integro-differential equation:
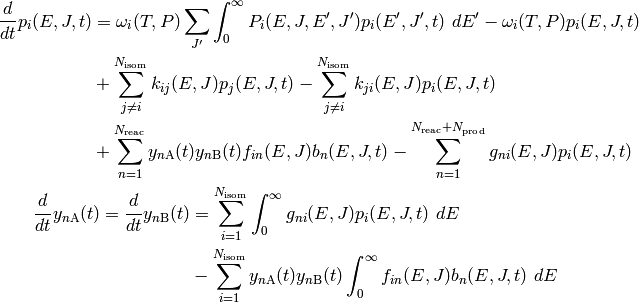
A summary of the variables is given below:
| Variable | Meaning |
|---|---|
 |
Population distribution of isomer 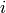 |
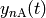 |
Total population of species 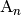 in reactant channel in reactant channel 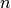 |
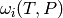 |
Collision frequency of isomer 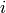 |
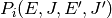 |
Collisional transfer probability from 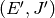 to to 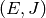 for isomer for isomer 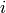 |
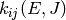 |
Microcanonical rate coefficient for isomerization from isomer 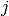 to isomer to isomer 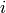 |
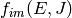 |
Microcanonical rate coefficient for association from reactant channel 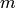 to isomer to isomer 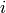 |
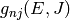 |
Microcanonical rate coefficient for dissociation from isomer 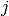 to reactant or product channel to reactant or product channel 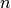 |
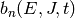 |
Boltzmann distribution for reactant channel 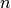 |
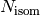 |
Total number of isomers |
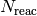 |
Total number of reactant channels |
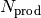 |
Total number of product channels |
The above is called the two-dimensional master equation because it contains two
dimensions: total energy 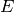 and total angular momentum quantum number
and total angular momentum quantum number
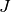 . In the first equation (for isomers), the first pair of terms
correspond to collision, the second pair to isomerization, and the final pair
to association/dissociation. Similarly, in the second equation above (for
reactant channels), the pair of terms refer to dissociation/association.
. In the first equation (for isomers), the first pair of terms
correspond to collision, the second pair to isomerization, and the final pair
to association/dissociation. Similarly, in the second equation above (for
reactant channels), the pair of terms refer to dissociation/association.
We can also simplify the above to the one-dimensional form, which
only has 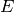 as a dimension:
as a dimension:
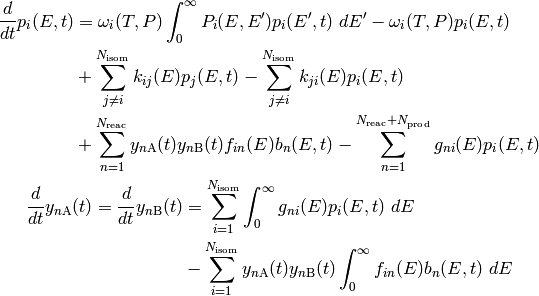
The equations as given are nonlinear, both due to the presence of the
bimolecular reactants and because both 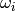 and
and
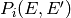 depend on the composition, which is changing with time.
The rate coefficients can be derived from considering the pseudo-first-order
situation where
depend on the composition, which is changing with time.
The rate coefficients can be derived from considering the pseudo-first-order
situation where 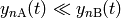 , and all
, and all
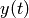 are negligible compared to the bath gas
are negligible compared to the bath gas 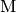 . From these
assumptions the changes in
. From these
assumptions the changes in 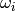 ,
, 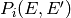 , and all
, and all
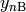 can be neglected, which yields a linear equation system.
can be neglected, which yields a linear equation system.
Except for the simplest of unimolecular reaction networks, both the one-dimensional and two-dimensional master equation must be solved numerically. To do this we must discretize and truncate the energy domain into a finite number of discrete bins called grains. This converts the linear integro-differential equation into a system of first-order ordinary differential equations:
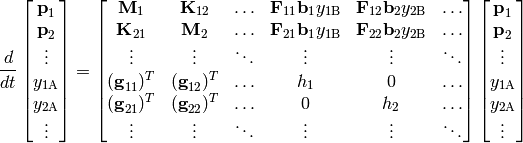
The diagonal matrices 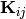 and
and 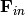 and
the vector
and
the vector 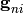 contain the microcanonical rate coefficients
for isomerization, association, and dissociation, respectively:
contain the microcanonical rate coefficients
for isomerization, association, and dissociation, respectively:
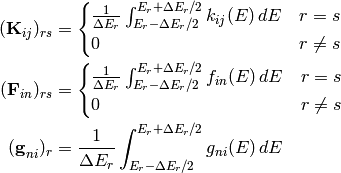
The matrices 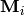 represent the collisional transfer
probabilities minus the rates of reactive loss to other isomers and to
reactants and products:
represent the collisional transfer
probabilities minus the rates of reactive loss to other isomers and to
reactants and products:
![(\matrix{M}_i)_{rs} = \begin{cases}
\omega_i \left[ P_i(E_r, E_r) - 1 \right] - \sum_{j \ne i}^{N_\mathrm{isom}} k_{ij}(E_r) - \sum_{n=1}^{N_\mathrm{reac} + N_\mathrm{prod}} g_{ni}(E_r) & r = s \\
\omega_i P_i(E_r, E_s) & r \ne s
\end{cases}](../_images/math/c2782450d7e6814d85aea4e92c0137837b1d3537.png)
The scalars 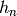 are simply the total rate coefficient for loss of
reactant channel
are simply the total rate coefficient for loss of
reactant channel 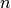 due to chemical reactions:
due to chemical reactions:
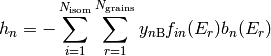
The interested reader is referred to any of a variety of other sources for alternative presentations, of which an illustrative sampling is given here [Gilbert1990] [Baer1996] [Holbrook1996] [Forst2003] [Pilling2003].
| [Gilbert1990] | R. G. Gilbert and S. C. Smith. Theory of Unimolecular and Recombination Reactions. Blackwell Sci. (1990). |
| [Baer1996] | T. Baer and W. L. Hase. Unimolecular Reaction Dynamics. Oxford University Press (1996). |
| [Holbrook1996] | K. A. Holbrook, M. J. Pilling, and S. H. Robertson. Unimolecular Reactions. Second Edition. John Wiley and Sons (1996). |
| [Forst2003] | W. Forst. Unimolecular Reactions: A Concise Introduction. Cambridge University Press (2003). |
| [Pilling2003] | M. J. Pilling and S. H. Robertson. Annu. Rev. Phys. Chem. 54, p. 245-275 (2003). doi:10.1146/annurev.physchem.54.011002.103822 |